Intervals level 5
In this guide...
Key terms:
Subscription required!
To view the complete study guide, you will need a valid subscription. Why not subscribe now?
Already have a subscription? Make sure you login first!
Introduction
We have looked at all of the possible intervals in the context of diatonic scales. This leaves just a few possibilities remaining, which we will now investigate.
Diatonic intervals
In Intervals level 4 we looked at all of the diatonic intervals. All of the intervals are defined using a two-word term:
- Number: The gap between the degrees of the scale that form the interval: 2nd, 3rd, 4th, 5th, 6th, or 7th
- Quality: Major, minor, augmented, diminished, or perfect
Using these two words, we are able to describe any of the intervals found in diatonic scales. Just to remind you:
- A fourth or fifth can be perfect, augmented, or diminished
- Any other interval can be major, minor, or augmented, or diminished (but not perfect!)
Chromatic intervals
Although the diatonic scales provide nearly all possible combinations of number and quality, there are a few intervals that you will not encounter in a diatonic scale. These intervals are only found when extra notes are used - notes from a chromatic scale.
You may find it useful to read The chromatic scale if you are unsure about the term "chromatic".
These extra possibilities are:
Augmented and diminished 3rd
We have seen augmented 2nds (between the 6th and 7th degrees of the harmonic minor scale), and plenty of augmented and diminished 5ths, but it is possible for any interval to be augmented or diminished.
The interval of the augmented 3rd is simply a major 3rd expanded or "augmented" by a semitone.
Likewise, the interval of the diminished 3rd is a minor 3rd reduced or "diminished" by a semitone.
We can therefore write down all four types of 3rd in order of semitone size:
 Diminished, minor, major, and augmented 3rds
Diminished, minor, major, and augmented 3rdsWe can draw up a similar series of sixths:
 Diminished, minor, major, and augmented 6ths
Diminished, minor, major, and augmented 6thsDiminished 2nd
You have already seen an augmented 2nd in the harmonic minor scale, but just as with 3rds, there is also the interval of the diminished 2nd. This is a somewhat unusual interval, because if you attempt to play it on an instrument, you'll discover that both notes sound at the same pitch!
This isn't a mistake and this interval really does exist, although it is quite rare. It is also not the same as a unison; for an interval to be a unison, both notes have to be identical in both name and pitch (e.g., C sharp and C sharp).
We can therefore write down all four types of 2nd in order of semitone size as follows. Try playing the diminished 2nd!
 Diminished, minor, major, and augmented 2nds
Diminished, minor, major, and augmented 2ndsSimilarly, here are the four types of 7th:
 Diminished, minor, major, and augmented 7ths
Diminished, minor, major, and augmented 7thsYou can see here that the augmented 7th, when played, sounds just like an octave - but just as the diminished 2nd is not a unison, the augmented 7th is not an octave!
4ths and 5ths
For completeness, here are all three versions of both the 4ths and 5ths:
 Diminished, minor, major, and augmented 4ths and 5ths
Diminished, minor, major, and augmented 4ths and 5thsThe key
We have not specified any key in the examples given above. All of the intervals have D as the lower note, but they do not need to be in D major, and indeed you would not find most of these intervals in D major.
For example, the augmented 4th D-G sharp is not in D major, but is found in both A major and A minor.
It is still essential to know whether the upper note would be present in a major or natural minor scale starting on the lower note.
Always remember to follow the two-step approach and describe number first, then quality:
- Identify the number: 2nd, 3rd, 4th, 5th, 6th, or 7th - how many steps from the lower note to the higher note?
- And after identifying the number, identify the quality: major, minor, perfect, augmented, diminished.
Identifying the quality requires you to know the major and minor scale starting on the lower note, as major intervals can be found in the major scale above the tonic and minor intervals in the minor scale above the tonic.
The only exception to this is the major 2nd and minor 2nd. The major 2nd is found above the tonic in both the major and minor scales. In this case, always remember that a major second is simply a tone and that a minor second is simply a semitone.
Some examples
Although it is quite easy to identify the number, the quality can be a little more tricky, so let's look at some examples and try to identify the intervals labelled A-D:
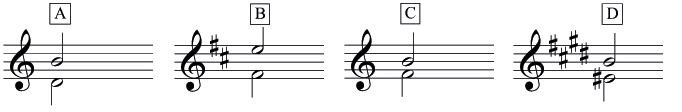 Four mystery intervals to identify
Four mystery intervals to identifyInterval A
- Number: Starting at D, you can count on your fingers D, E, F, G, A, B and reach the number 6, therefore this is a 6th.
- Quality: Is the upper note in D major? Yes; so this is a major 6th
- Double check the number of semitones: there are 9 semitones in a major 6th.
Interval B
Note that we have a key signature in this example that affects the notes in the interval!
- Number: Starting at F, count F, G, A, B, C, D, E and reach the number 7, therefore this is a 7th.
- Quality: Take into account the key signature! Is the upper note in F sharp major? - No. Is it in F sharp natural minor? - yes! So this is a minor 7th.
- Double check: 10 semitones
Interval C
- Number: Starting at F, count F, G, A, B and reach 4, therefore this is a 4th.
- Quality: Is it a perfect 4th - is the upper note in F major? - No. Is the upper note raised or lowered, compared to the note that should be in F major (B flat)? Raised; so this is an augmented 4th.
- Double check: 6 semitones.
Interval D
This is a tricky one!
- Number: Starting at E, count E, F, G, A, B and reach 5, therefore this is a 5th.
- Quality: Is it a perfect 5th - is the upper note in E sharp major?
Well, that is difficult because you won't instantly know the scale of E sharp major. So work for a moment in the enharmonic equivalent of F major; the perfect 5th would be F-C; and going back to "E sharp major" that would mean E sharp-B sharp. This is a B natural, and so it is not a perfect 5th. So what is it?
Is the upper note raised from the "perfect" note, B sharp? No. Is it lowered? Yes - B natural instead of B sharp.
Therefore, this is a diminished 5th.
Inverted intervals
Look again at these different types of 3rds and 6ths. This time, the bottom note of the 3rds is D, and the top note of the 6ths is D. Do you notice anything about these versions?
 Diminished, minor, major, and augmented 3rds and 6ths
Diminished, minor, major, and augmented 3rds and 6thsYou can see that all of the 3rds are based on D and (some kind of) F, and so too are the 6ths. We can pair these up so that the same F is in each - for example, there is D and F sharp in both the major 3rd and the minor 6th.
We call each interval in a pair the inversion of the other: D-F sharp is the inversion of F sharp-D, for example.
Any interval can be inverted like this simply by putting the bottom note at the top, and the following "opposites" appear:
| Number | Inversion |
|---|---|
| 2nd | 7th |
| 3rd | 6th |
| 4th | 5th |
| 5th | 4th |
| 6th | 3rd |
| 7th | 2nd |
| Quality | Inversion |
| Diminished | Augmented |
| Major | Minor |
| Minor | Major |
| Augmented | Diminished |
We can instantly see, therefore, what the inversion of any interval is. Look again at the 4ths and 5ths above, and the 2nds and 7ths, to see this for yourself.
This also shows why it is essential to describe an interval number by counting from the bottom note to the top (D, E, F = 3rd), and not from the top note to the bottom (F, G, A, B, C, D = 6th) - or you will end up with the inversion and have exactly the opposite of the right answer!
Compound intervals
So far we have simply counted intervals by number from a 2nd to a 7th. The interval after a 7th is of course an octave - but intervals don't stop there. They continue on and are described as a 9th, 10th, 11th and so on.
Rather than struggling to work out if an interval is an augmented 11th or diminished 9th, for example, it is useful to reduce the interval to its equivalent within one octave, by simply transposing the upper note down by an octave. In other words, a 9th is equivalent to an octave plus a 2nd, a 10th equivalent to an octave plus a 3rd, and so on.
These are called compound intervals: a major 10th is a compound major 3rd, a perfect 12th is a compound perfect 5th, and so on.
 Examples of compound intervals
Examples of compound intervalsFaced with an interval that is greater than an octave, begin by transposing the upper note down by an octave, and then proceed by the usual method to correctly name the interval. Remember, however, that to describe the interval fully, you must describe it as a compound interval - a compound augmented 5th, or a compound minor 3rd, for example.
Alternatively, after transposing the upper note down by an octave and working out the compound interval (for example, a compound perfect 4th) just add 7 to the interval's number (4 + 7 = 11), and then name the interval as a perfect 11th (leaving out the word "compound"). It is equally correct to say a perfect 11th or a compound perfect 4th.
Some examples
Here are three more mystery intervals to identify:
 Three mystery intervals to identify
Three mystery intervals to identifyInterval A
- Number: Starting at A, we count up to 9 (A, B, C, D, E, F, G, A, B) and so this is a 9th, or by transposing the top note down, we can see that this is a compound 2nd.
- Quality: This is a 2nd, so simply ask, is it a tone? No - it is a semitone. Therefore this is a compound minor 2nd or alternatively a minor 9th.
Interval B
We're in the bass clef now!
- Number: Starting at F, we count up to 13 to reach D, and so this is a 13th, or by transposing the top note down, we can see that this is a compound 6th.
- Quality: Is the upper note in F sharp major? No - it would have to be D sharp. Is the upper note in F sharp minor? No - that would be D natural.
Therefore, this is an augmented or diminished 6th. Is the top note higher than a major 6th would be (i.e., higher than D sharp)? No. Is it lower? Yes - therefore this is a compound diminished 6th or alternatively a diminished 13th.
Interval C
In this example, we have an accidental that over-rides the key signature. To complicate matters, each note is in a different clef.
- Number: Starting at G, we count up to 11, and so this is an 11th, or by transposing the top note down (both into the bass stave), a compound 4th.
- Quality: Is the upper note, C natural, in G major? Yes! Therefore this is a compound perfect 4th or alternatively a perfect 11th.
Beware!
There is a trap to watch out for when renaming compound intervals as the greater-than-an-octave equivalent. It is natural to think of an 11th as "an octave and a 4th" - which it is - and then to add 8 (for the octave) to 4, to get 12.
The interval is most definitely not a 12th - it is an 11th! - therefore be very careful to add 7 for an octave, and not 8.
For this reason, you might prefer to use the "compound Nth" description, instead of using numbers greater than 8, to describe an interval.
Read more...
With a subscription to Clements Theory you'll be able to read this and dozens of other study guides, along with thousands of practice questions and more! Why not subscribe now?
Revision
Are you sure you've understood everything in this study guide? Why not try the following practice questions, just to be sure!